SiFive Blog
The latest insights, and deeper technology dives, from RISC-V leaders

SiFive Accelerates RISC-V Vector Integration in XNNPACK for Optimized AI Inference
In this blog, we’ll begin by introducing XNNPACK and exploring its current status on RISC-V platforms. Next, to bridge the technical gap for contributors, we will provide a step-by-step guide on integrating RVV-optimized microkernels into XNNPACK, using F32-GEMM (single-precision floating-point general matrix multiplication) as a practical example. Finally, we will highlight the performance improvements achieved through these optimizations.
XNNPACK and status of RVV backend
XNNPACK is a crucial library-based solution for neural network inference on ARM, x86, and RISC-V platforms. It serves as a low-level acceleration backend for machine learning frameworks, such as TensorFlow Lite, PyTorch, ONNX Runtime, and MediaPipe. XNNPACK enhances performance by decomposing operations into microkernels and applying target-specific optimizations for each architecture.
Historically, XNNPACK offered limited support for RISC-V Vector (RVV) extension, providing only a small number of RVV-optimized microkernels. As a result, RISC-V users often had to rely on generic C implementations. To utilize vector hardware, users can only rely on auto-vectorizers for parallelization or translation headers or tools to adapt intrinsics from other platforms.
To enhance AI inference performance on RISC-V, SiFive has contributed several RVV-optimized floating-point microkernels to XNNPACK. They are listed in Table 1. These contributions significantly improve performance, making RISC-V a more viable platform for neural network inference. We welcome everyone to join us in XNNPACK RVV backend contributions.
| Microkernel Name | Description |
|---|---|
| F32-GEMM | Float 32-bit general matrix multiplication microkernel |
| F32-IGEMM | Float 32-bit indirect general matrix multiplication microkernel which is for Convolution |
| X32-PackW | Float or integer 32-bit weight packing |
| F32-rmin | Float 32-bit reduced min |
| F32-rmax | Float 32-bit reduced max |
| F32-rminmax | Float 32-bit reduced min and max |
| F32-vadd | Float 32-bit binary addition |
| F32-vsub | Float 32-bit binary subtract |
| F32-vrsub | Float 32-bit binary reverse-subtract |
| F32-vmul | Float 32-bit binary multiplication |
| F32-vdiv | Float 32-bit binary divide |
| F32-vrdiv | Float 32-bit binary reverse-divide |
| F32-vmax | Float 32-bit binary max |
| F32-vmin | Float 32-bit binary min |
| F32-vsqrdiff | Float 32-bit binary squared-of-difference |
| X32_transpose | Float or integer 32-bit transpose |
| F32_raddstoreexpminusmax | Float 32-bit exponent for softmax operation |
How to contribute the RVV microkernel to XNNPACK?
XNNPACK offers hundreds of microkernels to support neural network inference, with many neural network operations relying on one or more of these microkernels. For example, a fully_connected operator uses both weight-packing and GEMM (General Matrix Multiplication) microkernels. XNNPACK allows developers to implement target-specific microkernels, such as RVV (RISC-V Vector) versions of GEMM. If RVV and matrix extensions are available, alternative versions of GEMM microkernels can be developed.
Steps to contribute RVV microkernels:
- Identify the Operation and Relevant Microkernels
Start by determining which neural network operation and data type to optimize. Then, identify the relevant microkernels for that operation.
- Analyze the Microkernel Requirements
Understand the data layout assumptions and structure of the microkernel. Reviewing the scalar version can reveal important details. Note that certain data layouts are adjustable using microkernel parameters.
- Plan Vectorization Strategy and Select microkernel parameters
Develop a vectorization strategy and decide the suitable microkernel parameters to maximize performance.
- Implement the Target-Specific Microkernel Template
Rather than directly implementing the microkernel in C/C++, XNNPACK designs to create a target-specific template to increase flexibility. For example, design a template that supports different LMUL settings or register-tiling configurations. Once the template is complete, use a Python-based generator to produce C/C++ microkernels.
- Test and Benchmark the Microkernels
Validate each generated microkernel with unit tests and benchmark to find the most efficient version.
- Enable the Optimal Microkernel in Configuration
After identifying the best-performing microkernel, enable it in the configuration to ensure the operation uses the optimal microkernel at runtime.
Example: XNNPACK F32-GEMM optimization with RVV.
In this section, let’s take a floating-point fully_connected operation as an example. It is widely used in the Large language model and also the performance bottleneck.
We follow the steps in the last section:
-
Identify the Operation and Relevant Microkernels

Figure 1 The flow chart of floating-point fully_connected operation.
Based on Figure 1, there are two kinds of microkernels used in floating-point fully_connected operation. The first one is F32-GEMM. The other one is X32-PACKW, which stands for 32-bit weight packing. To simplify the article, we’ll focus on F32-GEMM in this blog.
-
Analyze the Microkernel Requirements
The GEMM microkernel has two input data layouts that must be understood for optimal implementation. Additionally, there are four key microkernel parameters—mr,nr,kr, andsr—that define its operation.
mrandnrdetermine the maximum output size for each iteration through thekdimension.- The Left-Hand Side (LHS) input,
A', has a data layout of[mr, k]. This means the F32-GEMM microkernel processes only a partial segment ofA, with themdimension of the input always being less than or equal tomr. - The Right-Hand Side (RHS) input,
packed_weight, has a layout influenced bynr,kr, andsr. Eachpacked_weighttile begins withnrbias values, followed by[k, nr]weight data, with its layout determined bykrandsr. - Figure 2 illustrates the data layout of
packed_weightwhennr=8andkr=sr=1. In this configuration, there areround_up(n, nr)packed_weighttiles. Each tile begins withnrbias values, followed by[k, nr]weights arranged in a row-major layout.

Figure 2 The data layout of packed_weightwhennr=8andkr=sr=1consists ofround_up(n, nr)tiles.
-
Plan Vectorization Strategy and Select microkernel parameters
Here, we aim to implement the outer product GEMM, settingkr = sr = 1. Our vectorization strategy focuses on vectorization along thendimension of the packed weight and output matrices. We usemrvector register groups as accumulators, along with one vector register group to load the packed weights. The application’s vector length(avl) is determined bynr, which is calculated based on the vector length (VLEN) and vector length multiplier (LMUL) settings:
nr = VLEN * LMUL / 32.
The values ofmrandLMULare defined by the input arguments of the template.Let’s explain the algorithm with an example: assume
mr = 7,nr = 64(withLMUL = 4,VLEN = 512), andk = 3. After iterating through all values ofK, we aim to producemr x nrresults.Step 1 (Figure 3):
The first step is to load the
nrbias values into the vector register group. These bias values are then duplicated across themraccumulator vector register groups.
Figure 3 RVV F32-GEMM outer product algorithm(part1).
Step 2 (Figure 4):
In each iteration over
K, we load themrscalar values into scalar registers (a0toa6). Then, we perform a vector load of the weight (v_w_k), followed by several vector floating-point multiplication-and-accumulation(vfmacc) instructions to compute the partial sum of the output.
Figure 4 RVV F32-GEMM outer product algorithm(part2).
Step 3 (Figure 5):
After iterating through all values of
K, we obtain output results with dimensions[mr, nr]. These results are stored inmrvector register groups, with each register containingnrelements. Finally, the results can be written to the output.
Figure 5 RVV F32-GEMM outer product algorithm(part3).
Steps 1 to 3 describe the procedure for calculating
[mr, nr]results. This process needs to be repeated for all the tiles inpacked_weightto obtain the entire output[mr, n].Note: If input
Ncannot be evenly divided bynr, we need to modify theavlfromnrtoN mod nrwhen tackling the last output tile. -
Implement the Target-Specific Microkernel Template
We developed an RVV f32-GEMM template that usesmrandLMULas configurable parameters.
-
Test and Benchmark the Microkernels
By generating code with various combinations ofmrandLMUL, we could comprehensively test and benchmark performance across multiple configurations.
-
Enable the Optimal Microkernel in Configuration
Based on benchmark results, we chose to enable an implementation withmr=7andLMUL=4, which maximizes vector register utilization and delivers optimal performance, in gemm-config. However, gemm-config is relatively complicated.If we want to enable RVV F32-gemm in configure. We also need to implement f32-igemm(indirect gemm) and corresponding x32-packw(weight packing) microkernels.
Performance Results
This section presents two types of experiments. The first involves microkernel-level benchmarks using the XNNPACK benchmark framework, while the second focuses on end-to-end model-level benchmarks through TensorFlow Lite. Both sets of experiments are conducted on the SiFive Intelligence X390 which supports RISC-V Vector and vector length (VLEN) is 1024. Three settings are evaluated:
- Setting 1: Pure scalar microkernels without auto-vectorization
- Setting 2: Pure scalar microkernels with auto-vectorization
- Setting 3: RVV intrinsic microkernels
OP-level
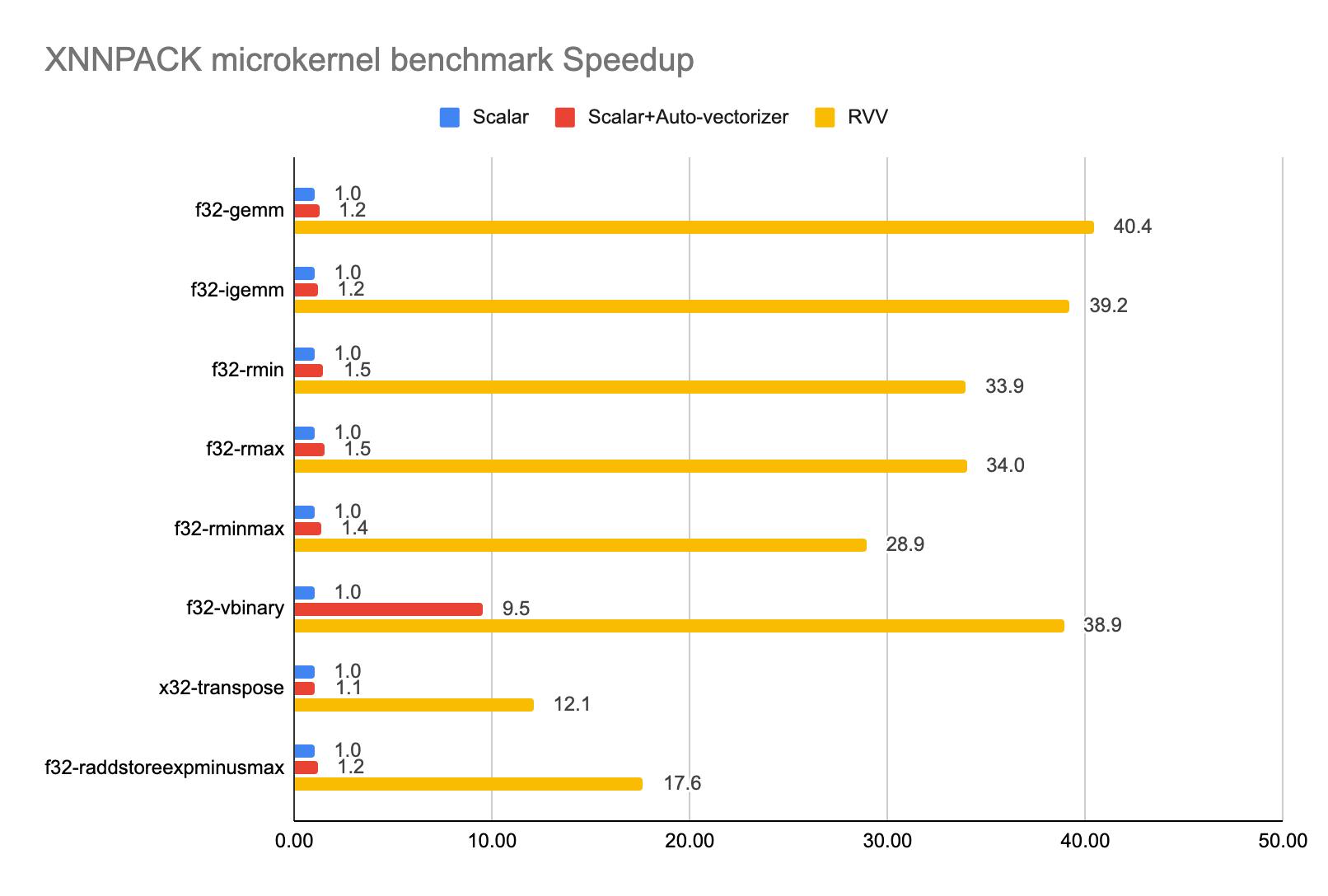
Figure 6. XNNPACK microkernel benchmark: performance speedup under different configurations on the SiFive Intelligence X390.
From the results in Figure 6, we observe that auto-vectorization provides only limited performance improvement. The primary reason is that most scalar code performs inner loop unrolling with a small size to emulate SIMD behavior commonly seen on x86 or ARM platforms. For example, in one of the reduced max microkernel calls, xnn_f32_rmax_ukernel__scalar_u4_acc4, the inner loop performs 4 binary max in parallel. This results in the auto-vectorizer generating code with a very small application vector length (AVL) of 4, which underutilizes the vector unit if vector length is large. To enhance auto-vectorization performance, rewriting the scalar source code is necessary. In contrast, the handwritten RVV-optimized code demonstrates better vector utilization and achieves a significant speedup compared to other approaches.
End-to-end benchmark using TFLite
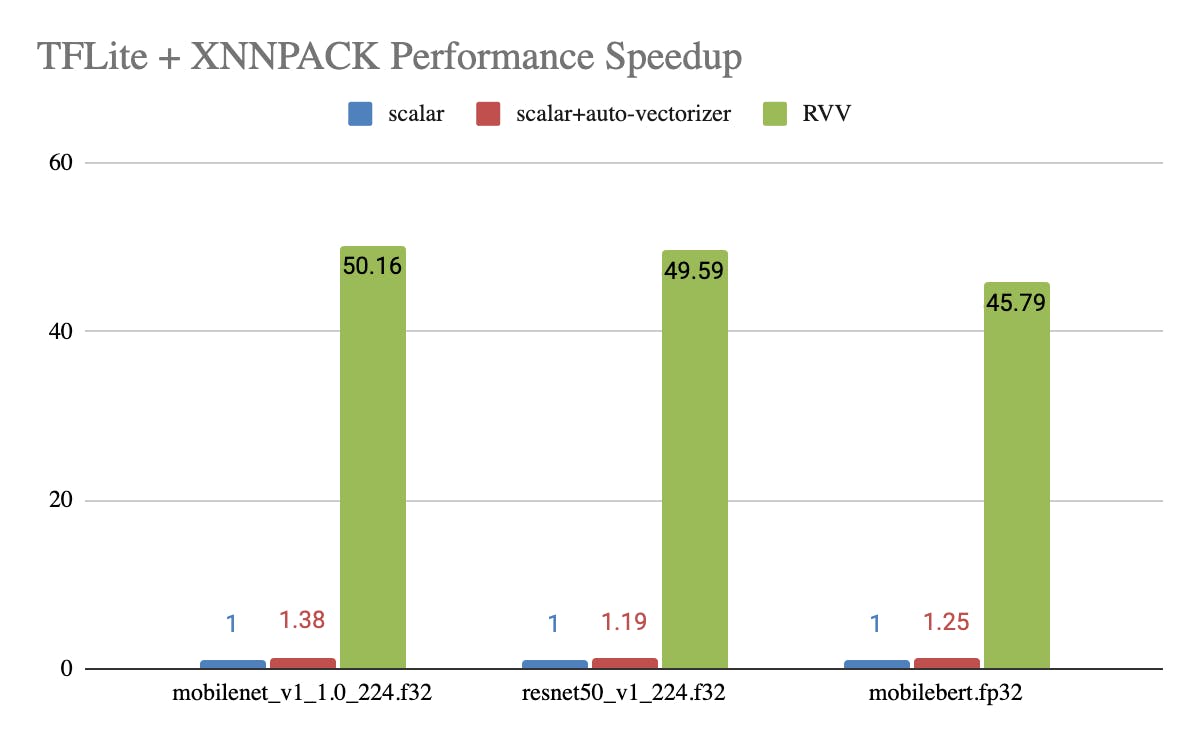
Figure 7. Performance speedup of using TFLite with XNNPACK across different ML models.
Figure 7 demonstrates performance speedups. It’s consistent with those observed in the XNNPACK benchmark. Specifically, transitioning from scalar to RVV achieves a speedup of over 45x, aligning with expected outcomes. Because the tested models are dominant to either F32-IGEMM or F32-GEMM. Both in the microkernel benchmark show a speedup of approximately 40x. Based on the performance results, we can conclude that optimizing XNNPACK RVV backend is a promising path.
Conclusion and Future Work
SiFive has provided optimizations for most of the critical single precision floating-point microkernels. The performance results are promising. However, XNNPACK isn't just for single precision floating-point neural network inference. There are still lots of microkernels that need to be optimized, such as the int8 version of GEMM, IGEMM and so on. We hope that RISC-V developers can join us in XNNPACK RVV backend contributions.
References
XNNPACK
https://github.com/google/XNNPACK
XNNPACK F32-GEMM pull request 1
https://github.com/google/XNNPACK/pull/5893
XNNPACK F32-GEMM pull request 2
https://github.com/google/XNNPACK/pull/6411
XNNPACK F32-GEMM pull request 3
https://github.com/google/XNNPACK/pull/7035
RISC-V Vector Extension specification
https://github.com/riscvarchive/riscv-v-spec/blob/master/v-spec.adoc#vector-byte-length-vlenb